Spin foams from arbitrary surfaces

by Frank Hellman, Albert Einstein Institute, Golm, Germany

Jacek Puchta, University of Warszaw
Title: The Feynman diagramatics for the spin foam models
PDF of the talk (3MB)
Audio [.wav 35MB], Audio [.aif 3MB].

In several previous blog posts (e.g. here) the spin foam approach to quantum gravity dynamics was introduced. To briefly summarize, this approach describes the evolution of a spin-network via a
2-dimensional surface that we can think of as representing how the network changes through time.


While this picture is intuitively compelling, at the technical level there have always been differences of opinions on what type of 2-dimensional surfaces should occur in this evolution. This question is particularly critical once we start trying to sum over all different type of surfaces. The original proposal for this 2-dimensional surface approach was due to Ooguri, who allowed only a very restricted set of surfaces, namely those called "dual to triangulations of manifolds".


A triangulation is a decomposition of a manifold into simplices. The simplices in successive dimensions are obtained by adding a point and "filling in". The 0-dimensional simplex is just a single point. For the 1-dimensional simplex we add a second point and fill in the line between them. For 2-dimensions we add a third point, fill in the space between the line and the third point, and obtain a triangle. In 3-d we get a tetrahedron, and in 4-d what is called a 4-simplex.


The surface "dual to a triangulation" is obtained by putting a vertex in the middle of the highest dimensional simplex, then connecting these by an edge for every simplex one dimension lower, and to fill in surfaces for every simplex two dimensions lower. An example for the case where the highest dimensional simplex is a triangle is given in the figure, there the vertex abc is in the middle of the triangle ABC, and connected by the dashed lines indicating edges, to the neighboring vertices.

All current spin foam models were created with such triangulations in mind. In fact many of the crucial results of the spin foam approach rely explicitly on this feature rather technical point.


The price we pay for restricting ourselves to such surfaces is that we do not address the dynamics of the full Loop Quantum Gravity Hilbert space. The spin networks we evolve will always be 4-valent, that is, there are always four links coming into every node, whereas in the LQG Hilbert space we have spin-networks of arbitrary valence. Another issue is that we might wish to study the dynamics of the model using the simplest surfaces first to get a feeling for what to expect from the theory, and for some interesting examples, like spin foam cosmology, the triangulation based surfaces are immediately quite complicated.


The group of Jerzy Lewandowski therefore suggested to generalize the amplitudes considered so far to fairly arbitrary surfaces, and gave a method for constructing the spin foam models, considered before in the triangulation context only, on these arbitrary surfaces. This patches one of the holes between the LQG kinematics and the spin foam dynamics. The price is that many of the geometricity results from before no longer hold.


Furthermore it now becomes necessary to effectively handle these general surfaces. A priori a lot of those exist, and it can be very hard to imagine them. In fact the early work on spin foam cosmology overlooked a large number of surfaces that potentially contribute to the amplitude. The work Jacek Puchta presented in this talk solves this issue very elegantly by developing a simple diagrammatic language that allows us to very easily work with these surfaces without having to imagine them.


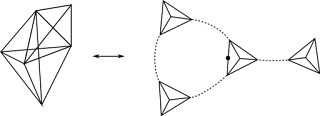
This is done by describing every node in the amplitude through a network, and then giving additional information that allows us to reconstruct a surface from these networks. Without going into the full details, consider a picture like in the next figure. The solid lines on the right hand side are the networks we consider, the dashed lines are additional data. Each node of the solid lines represents a triangle, every solid line is two triangles glued along an edge, and every dashed line is two triangles glued face to face. Following this prescription we obtain the triangulation on the left. While the triangulation generated by this prescription can be tricky to visualize in general, it is easy to work directly with the networks of dashed and solid lines. Furthermore we don't need to restrict ourselves to networks that generate triangulations anymore but can consider much more general cases.

This language has a number of very interesting features. First of all these networks immediately give us the spin-networks we need to evaluate to obtain the spin foam amplitude of the surface reconstructed from them.


Furthermore it is very easy to read off what the boundary spin network of a particular surface is. As a strong demonstration of how this language simplifies thinking about surfaces, he demonstrated how all surfaces relevant for the spin foam cosmology context, which were long overlooked, are easily seen and enumerated using the new language.


The challenge ahead is to understand whether the results obtained in the simplicial setting can be translated into the more general setting at hand. For the geometricity results this looks very challenging. But in any case, the new language looks like it is going to be an indispensable tool for studying spin foams going forward, and for clarifying the link between the canonical LQG approach and the covariant spin foams.

The Immirzi parameter in spin foam quantum gravity

by Sergei Alexandrov, Universite Montpellier, France.

James Ryan, Albert Einstein Institute
Title: Simplicity constraints and the role of the Immirzi parameter in quantum gravity
PDF of the talk (11MB)
Audio [.wav 19MB], Audio [.aif 2MB].


Spin foam quantization is an approach to quantum gravity. Firstly, it  is a "covariant" quantization, in that it does not break space-time into space and time as "canonical" loop quantum gravity (LQG) does. Secondly, it is "discrete" in that it assumes at the outset that space-time has a granular rather than a smooth structure assumed by "continuum" theories such as LQG. Finally, it is based on the "path integral" approach to quantization that Feynman introduced in which one sums probabilities for all possible trajectories in a system. In the case of gravity one assigns probabilities to all possible space-times.

To write the path integral in this approach one uses a reformulation of Einstein's general relativity due to Plebanski. Also, one examines this reformulation for discrete space-times. From the early days it was considered as a very close cousin of loop quantum gravity because both approaches lead to the same qualitative picture of quantum space-time.  (Remarkably, although one starts with smooth space and time in LQG, after quantization a granular structure emerges.)  However, at the quantitative level, for long time there was a striking disagreement. First of all, there were the symmetries.  On the one hand, LQG involves a set of symmetries known technically as the SU(2) group, while on the other, spin foam models had symmetries either associated with the SO(4) group or the Lorentz group. The latter are symmetries that emerge in space-time whereas the SU(2) symmetry emerges naturally in space. It is not surprising that working in a covariant approach the symmetries that emerge naturally are those of space-time whereas working in an approach where space is distinguished like in the canonical approach one gets symmetries associated with space. The second difference concerns the famous Immirzi parameter which plays an extremely important role in LQG, but was not even included in the spin foam approach. This is a parameter that appears in the classical formulation that has no observable consequences there (it amounts to a change of variables). On LQG quantization, however, physical predictions depend on it, in particular the value of the quantum of area and the entropy of black holes.

The situation has changed a few years ago with the appearance of two new spin foam models due to Engle-Pereira-Rovelli-Livine (EPRL) and Freidel-Krasnov (FK). The new models appear to agree with LQG at the kinematical level (i.e. they have similar state spaces, although their specific dynamics may differ). Moreover, they incorporate the Immirzi parameter in a non-trivial way.

The basic idea behind these models is the following: in the Plebanski formulation general relativity is represented as a topological BF theory supplemented by certain constraints ("simplicity constraints"). BF theories are well studied topological theories (their dynamics are very simple, being limited to global properties). This straightforwardness in particular implies that it is well known how to discretize and to quantize  BF theories (using, for example, the spin foam approach). The fact that general relativity can be thought of as a BF theory with additional constraints  gives rise to the idea that quantum gravity can be obtained by imposing the simplicity constraints directly at quantum level on a BF theory. For that purpose, using the standard quantization map of BF theories, the simplicity constraints become quantum operators acting on the BF states. The insight of EPRL was that, once the Immirzi parameter is included, some of the constraints should not be imposed as operator identities, but in a weaker form. This allows to find solutions of the quantum constraints which can be put into one-to-one correspondence with the kinematical states of LQG.

However, such quantization procedure does not take into account the fact that the simplicity constraints are not all the constraints of the theory. They should be supplemented by certain other ("secondary") constraints and together they form what is technically known as a system of second class constraints. These are very different from the usual kinds of constraints that appear in gauge theories. Whereas the latter correspond to the presence of symmetries in the theory, the former just freeze some degrees of freedom. In particular, at quantum level they should be treated in a completely different way. To implement second class constraints, one should either solve them explicitly, or use an elaborate procedure called the Dirac bracket. Unfortunately, in the spin foam approach the secondary constraints had been completely ignored so far.

At the classical level, if one takes all these constraints into account for continuum space-times, one gets a formulation which is independent of the Immirzi parameter. Such a canonical formulation can be used for a further quantization either by the loop or the spin foam method and leads to results which are still free from this dependence. This raises questions about the compatibility of the spin foam quantization with the standard Dirac quantization based on the continuum canonical analysis.

In this seminar James Ryan tried to shed light on this issue by studying a the canonical analysis of Plebanski formulation for discrete space-times. Namely, in his work with Bianca Dittrich, they analyzed constraints which must be imposed on the discrete BF theory to get a discretized geometry and how they affect the structure of the theory. They found that the necessary discrete constraints are in a nice correspondence with the primary and secondary simplicity constraints of the continuum theory.

Besides, it turned out that the independent constraints are naturally split into two sets. The first set expresses the equality of two sectors of the BF theory, which effectively reduces SO(4) gauge group to SU(2). And indeed, if one explicitly solves this set of constraints, one finds a space of states analogous to that of LQG and the new spin foam models dependent on the Immirzi parameter.

However, the corresponding geometries cannot be associated with piecewise flat geometries (geometries that are obtained by gluing flat simplices, just like one glues flat triangles to form a geodesic dome). These piecewise flat geometries are the geometries usually associated with spin foam models. Instead they produce the so called twisted geometries recently studied by Freidel and Speziale. To get the genuine discrete geometries appearing, for example, in the formulation of general relativity known as Regge calculus, one should impose an additional set of constraints given by certain gluing conditions. As Dittrich and Ryan succeeded in showing, the formulation obtained by taking into account all constraints is independent of the Immirzi parameter, as it is in the continuum classical formulation. This suggests that the quest for a consistent and physically acceptable spin foam model is far from being accomplished and that the final quantum theory might eventually be free from the Immirzi parameter.