Shape dynamics

by Julian Barbour, College Farm, Banbury, UK.


Tim Koslowski, Perimeter Institute 
Title: Shape dynamics
PDF of the talk (500k)
Audio [.wav 33MB], Audio [.aif 3MB].

I will attempt to give some conceptual background to the recent seminar by Tim Koslowski (pictured left) on Shape Dynamics and the technical possibilities that it may open up. Shape dynamics arises from a method, called best matching, by which motion and more generally change can be quantified. The method was first proposed in 1982, and its furthest development up to now is described here. I shall first describe a common alternative.

Newton’s Method of Defining Motion

Newton’s method, still present in many theoreticians’ intuition, takes space to be real like a perfectly smooth table top (suppressing one space dimension) that extends to infinity in all directions. Imagine three particles that in two instants form slightly different triangles (1 and 2). The three sides of each triangle define the relative configuration. Consider triangle 1. In Newtonian dynamics, you can locate and orient 1 however you like. Space being homogeneous and isotropic, all choices are on an equal footing. But 2 is a different relative configuration. Can one say how much each particle has moved? According to Newton, many different motions of the particles correspond to the same change of the relative configuration. Keeping the position of 1 fixed, one can place the centre of mass of 2, C2, anywhere; the orientation of 2 is also free. In three-dimensional space, three degrees of freedom correspond to the possible changes of the sides of the
triangle (relative data), three to the position of C2, and three to the orientation. The three relative data cannot be changed, but the choices made for the remainder are disturbingly arbitrary. In fact, Galilean relativity means
that the position of C2 is not critical. But the orientational data are crucial. Different choices for them put different angular momenta L into the system, and the resulting motions are very different. Two snapshots of relative configurations contain no information about L; you need three to get a handle on L. Now we consider the alternative.

Dynamics Based on Best Matching

The definition of motion by best matching is illustrated in the figure. Dynamics based on it is more restrictive than Newtonian dynamics. The reason can be ‘read off’ from the figure. Best matching, as shown in b, does two things. It brings the centers of mass of the two triangles to a common point and sets their net relative rotation about it to zero. This last means that a dynamical system governed by best matching is always constrained, in Newtonian terms, to have vanishing total angular momentum L. In fact, the dynamical equations are Newtonian; the constraint L = 0 is maintained by them if it holds at any one instant.

Figure 1. The Definition of Motion by Best Matching. Three particles, at the vertices of the grey and dashed triangles at two instants, move relative to each other. The difference between the triangles is fact, but can one determine unique displacements of the particles? It seems not. Even if we hold the grey triangle fixed in space, we can place the dashed triangle relative to it in any arbitrary position, as in a. There seems to be no way to define unique displacements. However, we can bring the dashed triangle into the position b, in which it most nearly ‘covers’ the grey triangle. A natural minimizing procedure determines when ‘best matching’ is achieved. The displacements that take one from the grey to the dashed triangle are not defined relative to space but relative to the grey triangle. The procedure is reciprocal and must be applied to the complete dynamical system under consideration.

So far, we have not considered size. This is where Shape Dynamics proper begins. Size implies the existence of a scale to measure it by. But, if our three particles are the universe, where is a scale to measure its size? Size is another Newtonian absolute. Best matching can be extended to include adjustment of the relative sizes. This is done for particle dynamics here. It leads to a further constraint. Not only the angular momentum but also something called the dilatational momentum must vanish. The dynamics of any universe governed by best matching becomes even more restrictive than Newtonian dynamics.

Best Matching in the Theory of Gravity

Best matching can be applied to the dynamics of geometry and compared with Einstein's general relativity (GR), which was created as a description of the four-dimensional geometry of spacetime. However, it can be reformulated as a dynamical theory in which three-dimensional geometry (3-geometry) evolves. This was done in the late 1950s by Dirac and Arnowitt, Deser, and Misner (ADM), who found a particularly elegant way to do it that is now called the ADM formalism and is based on the Hamiltonian form of dynamics. In the ADM formalism, the diffeomorphism constraint, mentioned a few times by Tim Koslowski, plays a prominent role. Its presence can be explained by a sophisticated generalization of the particle best matching shown in the figure. This shows that the notion of change was radically modified when Einstein created GR (though this fact is rather well hidden in the spacetime formulation). The notion of change employed in GR means that it is background independent . In the ADM formalism as it stands, there is no constraint that corresponds to best matching with respect to size. However, in addition to the diffeomorphism constraint, or rather constraints as there are infinitely many of them, there are also infinitely many Hamiltonian constraints. They reflect the absence of an external time in Einstein's theory and the almost complete freedom to define simultaneity at spatially separated points in the universe. It has proved very difficult to take them into account in a quantum theory of gravity. Building on previous work, Tim and his collaborators Henrique Gomes and Sean Gryb have found an alternative Hamiltonian representation of dynamical geometry in which all but one of the Hamiltonian constraints can be swapped for conformal constraints. These conformal constraints arise from a best matching in which the volume of space can be adjusted with infinite flexibility. Imagine a balloon with curves drawn on it that form certain angles wherever they meet. One can imagine blowing up the balloon or letting it contract by different amounts everywhere on its surface. In this process, the angles at which the curves meet cannot change, but the distances between points can. This is called a conformal transformation and is clearly analogous to changing the overall size of figures in Euclidean space. The conformal transformations that Tim discusses in his talk are applied to curved 3-geometries that close up on themselves like the surface of the earth does in two dimensions. The alternative, or dual, representation of gravity through the introduction of conformal best matching seems to open up new routes to quantum gravity. At the moment, the most promising looks to be the symmetry doubling idea discussed by Tim. However, it is early days. There are plenty of possible obstacles to progress in this direction, as Tim is careful to emphasize. One of the things that intrigues me most about Shape Dynamics is that, if we are to explain the key facts of cosmology by a spatially closed expanding universe, we cannot allow completely unrestricted conformal transformations in the best matching but only the volume-preserving ones (VPCTs) that Tim discusses. This is a tiny restriction but strikes me as the very last vestige of Newton's absolute space. I think this might be telling us something fundamental about the quantum mechanics of the universe. Meanwhile it is very encouraging to see technical possibilities emerging in the new conceptual framework.

Spin foams from arbitrary surfaces

by Frank Hellman, Albert Einstein Institute, Golm, Germany

Jacek Puchta, University of Warszaw
Title: The Feynman diagramatics for the spin foam models
PDF of the talk (3MB)
Audio [.wav 35MB], Audio [.aif 3MB].

In several previous blog posts (e.g. here) the spin foam approach to quantum gravity dynamics was introduced. To briefly summarize, this approach describes the evolution of a spin-network via a
2-dimensional surface that we can think of as representing how the network changes through time.


While this picture is intuitively compelling, at the technical level there have always been differences of opinions on what type of 2-dimensional surfaces should occur in this evolution. This question is particularly critical once we start trying to sum over all different type of surfaces. The original proposal for this 2-dimensional surface approach was due to Ooguri, who allowed only a very restricted set of surfaces, namely those called "dual to triangulations of manifolds".


A triangulation is a decomposition of a manifold into simplices. The simplices in successive dimensions are obtained by adding a point and "filling in". The 0-dimensional simplex is just a single point. For the 1-dimensional simplex we add a second point and fill in the line between them. For 2-dimensions we add a third point, fill in the space between the line and the third point, and obtain a triangle. In 3-d we get a tetrahedron, and in 4-d what is called a 4-simplex.


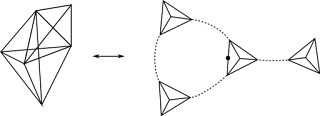
The surface "dual to a triangulation" is obtained by putting a vertex in the middle of the highest dimensional simplex, then connecting these by an edge for every simplex one dimension lower, and to fill in surfaces for every simplex two dimensions lower. An example for the case where the highest dimensional simplex is a triangle is given in the figure, there the vertex abc is in the middle of the triangle ABC, and connected by the dashed lines indicating edges, to the neighboring vertices.

All current spin foam models were created with such triangulations in mind. In fact many of the crucial results of the spin foam approach rely explicitly on this feature rather technical point.


The price we pay for restricting ourselves to such surfaces is that we do not address the dynamics of the full Loop Quantum Gravity Hilbert space. The spin networks we evolve will always be 4-valent, that is, there are always four links coming into every node, whereas in the LQG Hilbert space we have spin-networks of arbitrary valence. Another issue is that we might wish to study the dynamics of the model using the simplest surfaces first to get a feeling for what to expect from the theory, and for some interesting examples, like spin foam cosmology, the triangulation based surfaces are immediately quite complicated.


The group of Jerzy Lewandowski therefore suggested to generalize the amplitudes considered so far to fairly arbitrary surfaces, and gave a method for constructing the spin foam models, considered before in the triangulation context only, on these arbitrary surfaces. This patches one of the holes between the LQG kinematics and the spin foam dynamics. The price is that many of the geometricity results from before no longer hold.


Furthermore it now becomes necessary to effectively handle these general surfaces. A priori a lot of those exist, and it can be very hard to imagine them. In fact the early work on spin foam cosmology overlooked a large number of surfaces that potentially contribute to the amplitude. The work Jacek Puchta presented in this talk solves this issue very elegantly by developing a simple diagrammatic language that allows us to very easily work with these surfaces without having to imagine them.


This is done by describing every node in the amplitude through a network, and then giving additional information that allows us to reconstruct a surface from these networks. Without going into the full details, consider a picture like in the next figure. The solid lines on the right hand side are the networks we consider, the dashed lines are additional data. Each node of the solid lines represents a triangle, every solid line is two triangles glued along an edge, and every dashed line is two triangles glued face to face. Following this prescription we obtain the triangulation on the left. While the triangulation generated by this prescription can be tricky to visualize in general, it is easy to work directly with the networks of dashed and solid lines. Furthermore we don't need to restrict ourselves to networks that generate triangulations anymore but can consider much more general cases.

This language has a number of very interesting features. First of all these networks immediately give us the spin-networks we need to evaluate to obtain the spin foam amplitude of the surface reconstructed from them.


Furthermore it is very easy to read off what the boundary spin network of a particular surface is. As a strong demonstration of how this language simplifies thinking about surfaces, he demonstrated how all surfaces relevant for the spin foam cosmology context, which were long overlooked, are easily seen and enumerated using the new language.


The challenge ahead is to understand whether the results obtained in the simplicial setting can be translated into the more general setting at hand. For the geometricity results this looks very challenging. But in any case, the new language looks like it is going to be an indispensable tool for studying spin foams going forward, and for clarifying the link between the canonical LQG approach and the covariant spin foams.

The Immirzi parameter in spin foam quantum gravity

by Sergei Alexandrov, Universite Montpellier, France.

James Ryan, Albert Einstein Institute
Title: Simplicity constraints and the role of the Immirzi parameter in quantum gravity
PDF of the talk (11MB)
Audio [.wav 19MB], Audio [.aif 2MB].


Spin foam quantization is an approach to quantum gravity. Firstly, it  is a "covariant" quantization, in that it does not break space-time into space and time as "canonical" loop quantum gravity (LQG) does. Secondly, it is "discrete" in that it assumes at the outset that space-time has a granular rather than a smooth structure assumed by "continuum" theories such as LQG. Finally, it is based on the "path integral" approach to quantization that Feynman introduced in which one sums probabilities for all possible trajectories in a system. In the case of gravity one assigns probabilities to all possible space-times.

To write the path integral in this approach one uses a reformulation of Einstein's general relativity due to Plebanski. Also, one examines this reformulation for discrete space-times. From the early days it was considered as a very close cousin of loop quantum gravity because both approaches lead to the same qualitative picture of quantum space-time.  (Remarkably, although one starts with smooth space and time in LQG, after quantization a granular structure emerges.)  However, at the quantitative level, for long time there was a striking disagreement. First of all, there were the symmetries.  On the one hand, LQG involves a set of symmetries known technically as the SU(2) group, while on the other, spin foam models had symmetries either associated with the SO(4) group or the Lorentz group. The latter are symmetries that emerge in space-time whereas the SU(2) symmetry emerges naturally in space. It is not surprising that working in a covariant approach the symmetries that emerge naturally are those of space-time whereas working in an approach where space is distinguished like in the canonical approach one gets symmetries associated with space. The second difference concerns the famous Immirzi parameter which plays an extremely important role in LQG, but was not even included in the spin foam approach. This is a parameter that appears in the classical formulation that has no observable consequences there (it amounts to a change of variables). On LQG quantization, however, physical predictions depend on it, in particular the value of the quantum of area and the entropy of black holes.

The situation has changed a few years ago with the appearance of two new spin foam models due to Engle-Pereira-Rovelli-Livine (EPRL) and Freidel-Krasnov (FK). The new models appear to agree with LQG at the kinematical level (i.e. they have similar state spaces, although their specific dynamics may differ). Moreover, they incorporate the Immirzi parameter in a non-trivial way.

The basic idea behind these models is the following: in the Plebanski formulation general relativity is represented as a topological BF theory supplemented by certain constraints ("simplicity constraints"). BF theories are well studied topological theories (their dynamics are very simple, being limited to global properties). This straightforwardness in particular implies that it is well known how to discretize and to quantize  BF theories (using, for example, the spin foam approach). The fact that general relativity can be thought of as a BF theory with additional constraints  gives rise to the idea that quantum gravity can be obtained by imposing the simplicity constraints directly at quantum level on a BF theory. For that purpose, using the standard quantization map of BF theories, the simplicity constraints become quantum operators acting on the BF states. The insight of EPRL was that, once the Immirzi parameter is included, some of the constraints should not be imposed as operator identities, but in a weaker form. This allows to find solutions of the quantum constraints which can be put into one-to-one correspondence with the kinematical states of LQG.

However, such quantization procedure does not take into account the fact that the simplicity constraints are not all the constraints of the theory. They should be supplemented by certain other ("secondary") constraints and together they form what is technically known as a system of second class constraints. These are very different from the usual kinds of constraints that appear in gauge theories. Whereas the latter correspond to the presence of symmetries in the theory, the former just freeze some degrees of freedom. In particular, at quantum level they should be treated in a completely different way. To implement second class constraints, one should either solve them explicitly, or use an elaborate procedure called the Dirac bracket. Unfortunately, in the spin foam approach the secondary constraints had been completely ignored so far.

At the classical level, if one takes all these constraints into account for continuum space-times, one gets a formulation which is independent of the Immirzi parameter. Such a canonical formulation can be used for a further quantization either by the loop or the spin foam method and leads to results which are still free from this dependence. This raises questions about the compatibility of the spin foam quantization with the standard Dirac quantization based on the continuum canonical analysis.

In this seminar James Ryan tried to shed light on this issue by studying a the canonical analysis of Plebanski formulation for discrete space-times. Namely, in his work with Bianca Dittrich, they analyzed constraints which must be imposed on the discrete BF theory to get a discretized geometry and how they affect the structure of the theory. They found that the necessary discrete constraints are in a nice correspondence with the primary and secondary simplicity constraints of the continuum theory.

Besides, it turned out that the independent constraints are naturally split into two sets. The first set expresses the equality of two sectors of the BF theory, which effectively reduces SO(4) gauge group to SU(2). And indeed, if one explicitly solves this set of constraints, one finds a space of states analogous to that of LQG and the new spin foam models dependent on the Immirzi parameter.

However, the corresponding geometries cannot be associated with piecewise flat geometries (geometries that are obtained by gluing flat simplices, just like one glues flat triangles to form a geodesic dome). These piecewise flat geometries are the geometries usually associated with spin foam models. Instead they produce the so called twisted geometries recently studied by Freidel and Speziale. To get the genuine discrete geometries appearing, for example, in the formulation of general relativity known as Regge calculus, one should impose an additional set of constraints given by certain gluing conditions. As Dittrich and Ryan succeeded in showing, the formulation obtained by taking into account all constraints is independent of the Immirzi parameter, as it is in the continuum classical formulation. This suggests that the quest for a consistent and physically acceptable spin foam model is far from being accomplished and that the final quantum theory might eventually be free from the Immirzi parameter.

What is hidden in an infinity?

by Daniele Oriti, Albert Einstein Institute, Golm, Germany


Matteo Smerlak, ENS Lyon
Title: Bubble divergences in state-sum models
PDF of the slides (180k)
Audio [.wav 25MB], Audio [.aif 5MB].

Physicists tend to dislike infinities. In particular, they take it very badly when the result of a calculation they are doing turns out to be not some number that they could compare with experiments, but infinite. No energy or distance, no velocity or density, nothing in the world around us has infinity as its measured value. Most  times, such infinities signal that we have not been smart enough in dealing with the physical system we are considering, that we have missed some key ingredient in its description, or used the wrong mathematical language in describing it. And we do not like to be reminded of our own lack of cleverness.

At the same time, and as a confirmation of the above, much important progress in theoretical physics has come out of a successful intellectual fight with infinities. Examples abound, but here is a historic one. Consider a large 3-dimensional hollow spherical object whose inside is made of some opaque material (thus absorbing almost all the light hitting it), and assume that it is filled with light (electromagnetic radiation) maintained at constant temperature. This object is named a black body. Imagine now that the object has a small hole from which a limited amount of light can exit. If one computes the total energy (i.e. considering all possible frequencies) of the radiation exiting from the hole, at a given temperature and at any given time, using the well-established laws of classical electromagnetism and classical statistical mechanics, one finds that it is infinite. Roughly, this calculation looks as follows: you have to sum all the contributions to the total energy of the radiation emitted (at any given time), coming from all the infinite modes of oscillation of the radiation, at the temperature T. Since there are infinite modes, the sum diverges. Notice that the same calculation can be performed by first imagining that there exists a maximum possible mode of oscillation, and then studying what
happens when this supposed maximum is allowed to grow indefinitely. After the first step, the calculation gives a finite result, but the original divergence is obtained again after the second step. In any case, this sum gives a divergent result: infinity! However, this two-step procedure allows to understand better how the quantity of interest diverges.

Beside being a theoretical absurdity, this is simply false on experimental grounds since such radiating objects can be realized rather easily in a laboratory. This represented a big crisis in classical physics at the end of the 19th century. The solution came from Max Planck with the hypothesis that light is in reality constituted by discrete quanta (akin to matter particles), later named photons, with a consequently different formula for the emitted radiation from the hole (more precisely, for the individual contributions). This hypothesis, initially proposed for completely different motivations, not only solved the paradox of the infinite energy, but spurred the quantum mechanics revolution which led (after the work of Bohr, Einstein, Heisenberg, Schroedinger, and many others) to the modern understanding of light, atoms and all fundamental forces (except gravity).

We see, then, that the need to understand what was really lying inside an infinity, the need to confront it, led to an important jump forward in our understanding of Nature (in this example, of light), and to a revision of our most cherished assumptions about it. The infinity was telling us just that. Interestingly, a similar theoretical phenomenon seems now to suggest that another, maybe even greater jump forward is needed and a new understanding of gravity and of spacetime itself.

An object that is theoretically very close to a perfect black body is a black hole. Our current theory of matter, quantum field theory, in conjunction with our current theory of gravity, General Relativity, predicts that such black hole will emit thermal radiation at a constant temperature inversely proportional to the mass of the black hole. This is called Hawking radiation. This result, together with the description of black holes provided by general relativity, also suggest that black holes have an entropy associated to them, measuring the number of their intrinsic degrees of freedom. Because a black hole is nothing but a particular configuration of space, this entropy is then a measure of the intrinsic degrees of freedom of (a region of) space itself! However, first of all we have no real clue what these intrinsic degrees of freedom are; second, if the picture of space provided by general relativity is correct, their number and their corresponding entropy is infinite!

This fact, together with a large number of other results and conceptual puzzles, prompted a large part of the theoretical physics community to look for a better theory of space (and time), possibly based on quantum mechanics (taking on board the experience from history): a quantum theory of space-time, a quantum theory of gravity.

It should not be understood that the transition from classical to quantum mechanics led us away from the problem of infinities in physics. On the contrary, our best theories of matter and of fundamental forces, quantum field theories, are full of infinities and divergent quantities. What we have learned, however, from quantum field theories, is exactly how to deal with such infinities in rather general terms, what to expect, and what to do when such infinities present themselves. In particular, we have learned another crucial lesson about nature: physical phenomena look very different at different energy and distance scales, i.e. if we look at them very closely or if they involve higher and higher energies. The methods by which we deal with this scale dependence go under the name of renormalization group, now a crucial ingredient of all theories of particles and materials, both microscopic and macroscopic. How this scale dependence is realized in practice depends of course on the specific physical system considered.

Let us consider a simple example. Consider the dynamics of a hypothetical particle with mass m and no spin; assume that what can happen to this particle during its evolution is only one of the following two possibilities: it can either disintegrate into two new particles of the same type or disintegrate into three particles of the same type. Also, assume that the inverse processes are also allowed (that is, two particles can disappear and give rise to a single new one, and the same can do three particles). So there are two possible ‘interactions’ that this type of particle can undergo, two possible fundamental processes that can happen to it. To each of them, we associate a parameter, called a ‘coupling constant’ that indicates how strong each possible interaction process is (compared with each other and with other possible processes due for example to the interaction of the particles with gravity or with light etc), one for the process involving three particles, and one for the one involving four  particles (this is counting incoming and outgoing particles). Now, the basic object that a quantum field theory allows us to compute is the probability (amplitude) that, if I first see a number n of particles at a certain time, at a later time I will instead see m particles, with m different from n (because some particle will have disintegrated and other will have been created). All the other quantities of physical interest can be obtained using these probabilities.

Moreover, the theory tells me exactly how this probability should be computed. It goes roughly as follows. First, I have to consider all possible processes leading from n particles to m particles, including those involving an infinite number of elementary creation/disintegration processes. These can be represented by graphs (called Feynman graphs) in which each vertex represents a possible elementary process (see the figure for an example of such process, made out of interactions involving three particles only, with associated graph,).

A graph describing a sequence of 3-valent elementary interactions for a point particle, with 2 particles measured both at the initial and at the final time (to be read from left to right)


Second, each of these processes should be assigned a probability (amplitude), that is, a function of the mass of the particle considered and of the ‘coupling constants’. Third, this amplitude is in turn a function of the energies of each particle involved in any given process.(and corresponding to a single line in the graph representing the process), and this energy can be anything, from zero to infinity. The theory tells me what form the probability amplitude has. Now the total probability for the measurement of n particle first and m particles later is computed by summing over all processes/graphs (including those composed of infinite elementary processes) and all the energies of particles involved in them, weighted by the probability amplitudes.

Now, guess what? The above calculation typically gives the always feared result: infinity. Basically, everything that could go wrong, actually goes wrong, as in Murphy’s law. Not only the sum over all the graphs/processes gives a divergent answer, but also the intermediate sum over energies diverges. However, as we anticipated, we now know how to deal with this kind of infinities, we are not scared anymore and, actually, we have learnt what they mean, physically. The problem mainly arises when we consider higher and higher energies for the particles involved in the process. For simplicity imagine that all the particles have the same energy E, and assume this can take any value from 0 to a maximum value Emax. Just like in the black body example, the existence of the maximum implies that the sum over energies is a finite number, so everything up to here goes fine. However, when we let the maximal energy becomes infinite, typically the same quantity becomes infinite.

We have done something wrong; let’s face it: there is something we have not understood of the physics of the system (simple particles as they may be). It could be that, as in the case of the blackbody radiation, we are missing something fundamental about the nature of these particles, and we have to change the whole probability amplitude. Maybe other type of particles have to be considered as created out of the initial ones. All this could be. However, what quantum field theory has taught us is that, before considering these more drastic possibilities, one should try to re-write the above calculation by considering coupling constants and mass, that themselves depend on the scale Emax, and then compute again the probability amplitude, but now using these ‘scale dependent’constants, and check if one can now consider the case of Emax growing up to infinity, i.e. consider arbitrary energies for the particles involved in the process. If this can be done, i.e. if one can find coupling constants dependent on the energies such that now the result of sending Emax to infinity, i.e. considering larger and larger energies, is a finite, sensible probability then there no need for further modifications of the theory, and the physical system considered, i.e. the (system of) particles, is under control.

What does all this teach us? It teaches us that the type of interactions that the system can
undergo and their relative strengths depend on the scale at which we look at the system, i.e. on what energy is involved in any process the system is experiencing. For example, it could happen that when Emax becomes higher and higher, the coupling constant as a function of Emax becomes zero. This would mean that, at very high energies, the process of disintegration of one particle into two (or two into one) does not happen anymore, and only the one involving four particles takes place. Pictorially, only graphs of a certain shape, become relevant. Or, it could happen that, at very high energies, the mass of the particles becomes zero,
i.e. the particles become lighter and lighter, eventually propagating just like photons do. The general lesson, beside technicalities and specific cases, is that for any given physical system it is crucial to understand exactly how the quantities of interest diverge, because in the details of such divergence lies important information about the true physics of the system considered. The infinities in our models should be tamed, explored in depth, and listened to.

This is what Matteo Smerlak and Valentin Bonzom have done in the work presented at the seminar, for some models of quantum space that are currently at the center of attention of the quantum gravity community. These are so-called spin foam models, in which quantum space is described in terms of spin networks (graphs whose links are assigned discrete numbers, spins, representing elementary geometric data) or equivalently in terms of collections of triangles glued to one another along edges, and whose geometry is specified by the length of all such edges. Spin foam models are then strictly related to both loop quantum gravity, whose dynamical aspects they seek to define, and to other approaches to quantum gravity like simplicial gravity. These models, very much like models for the dynamics of ordinary quantum particles, aim to compute (among other things) the probability to measure a given configuration of quantum space, represented again as a bunch of triangles glued together or as a spin network graph. Notice that here a ‘configuration of quantum space’ means both a given shape of space (it could be a sphere, a doughnut, or any other fancier shape), and a given geometry (it could be a very big or a very small sphere, a sphere with some bumps here and there, etc). One could also consider computing the probability of a transition from a given configuration of quantum space to a different one.

More precisely, the models that Bonzom and Smerlak studied are simplified ones (with respect to those that aim at describing our 4-dimensional space-time) in which the dynamics is such that, whatever the shape and geometry of space one is considering, during its evolution, should one measure the curvature of the same space at any given location, one would find zero. In other words these models only consider flat space-times. This is of course a drastic simplification but not such that the resulting models become uninteresting. On the contrary, these flat models are not only perfectly fine to describe quantum gravity in the case in which space has only two dimensions, rather than three, but are also the very basis for constructing realistic models
for 3-dimensional quantum space, i.e. 4-dimensional quantum spacetime. As a consequence, these models, together with the more realistic ones, have been a focus of attention of the community of quantum gravity researchers.

What is the problem being discussed, then? As you can imagine, the usual one: when one tries to compute the mentioned probability for a certain evolution of quantum space, even within these simplified models, the answer one gets is the ever-present, but by now only slightly intimidating, infinity. How does the calculation look like? It looks very similar to the calculation for the probability of a given process of evolution of particles in quantum field theory. Consider the case in which space is 2-dimensional and therefore space-time is 3-dimensional. Suppose you want to consider the probability of measuring first n triangles glued along one another to form, say, a 2-dimensional sphere (the surface of a soccer ball) of a given size, and then m triangles now glued to form, say, the surface of a doughnut. Now take a collection of an arbitrary number of triangles and glue them to one another along edges to form a 3-dimensional object of your choice, just like kids stick LEGO blocks to one another to form a house or a car or some spaceship (you see, science is in many ways the development of children’s curiosity by other means). It could be as simple as a soccer ball, in principle, or something extremely complicated, with holes, multiple connections, anything). There is only one condition on the 3-dimensional object you can build: its surface should be formed, in the example we are considering here, by two disconnected parts: one in the shape of a sphere made of n triangles, and one in the shape of the surface of a doughnut made of m triangles. This condition would for example prevent you from building a soccer ball, which you could do, instead, if one wanted to consider only the probability of measuring n triangles forming a sphere, and no doughnut was involved. Too bad. We’ll be lazy in this example and consider a doughnut but no soccer ball. Anyway, apart from this, you can do anything.

Let us pause for a second to clarify what it means for a space to have a given shape. Consider a point on the sphere and take a path on it that starts at the given point and after a while comes back to the same point, forming a loop. Now you see that there is no problem in taking this loop to become smaller and smaller, eventually shrinking to a point and disappearing. Now do the same operation on the surface of a doughnut. You will see that certain loops can again be shrunk to a point and made disappear, while others cannot. These are the ones that go around the hole of the doughnut. So you see that operations like these can help us determining the shape of our space. The same holds true for 3d spaces, in fact, you only need many more types of operations of this type. Ok, now you finish building your 3-dimensional object made of as many triangles as you want. Just as the triangles in the boundary of the 3d object, those forming the sphere and the doughnut, also those forming the 3d object come with numbers associated to the edges of the triangles. These numbers, as said, specify the geometry of all the triangles, and therefore of the sphere, of the doughnut and of the 3d object that has them on its boundary.

A collection of glued triangles forming a sphere (left) and a doughnut (right); the interior 3d space can alsobe built out of glued triangles having the given shape on the boundary: for the first object, the interior is a ball; for the second it forms what is called a solid torus. Pictures from http://www.hakenberg.de/

The theory (the spin foam model you are studying) should give you a probability for the process considered. If the triangles forming the sphere represent how quantum space was at first, and the triangles forming the doughnut how it is in the end, the 3d object chosen represent a possible quantum space-time. In the analogy with the particle process described earlier, the n triangles forming a sphere correspond to the initial n particles, the m triangles forming the doughnut correspond to the final m particles, and the triangulated 3d object is the analogue of a possible ‘interaction process’, a possible history of triangles being created/destroyed, forming different shapes and changing their size; this size is encoded in their edge lengths, which is the analogue of the energies of the particles. The spin foam model now gives you the probability for the process in the form of a sum over the probabilities for all possible assignments of lengths to the edges of the 3d object, each probability function enforcing that the 3d object is flat (it gives probability equal to zero if the 3d object is not flat). As anticipated, the above calculation gives the usual nonsensical infinity as a result. But again, we now know that we should get past the disappointment, and look more carefully at what this infinity hides. So what one does is again to imagine that there is a maximal length that edges of triangles can have, call it Emax, define the truncated amplitude and study carefully exactly how it behaves when Emax grows, when it is allowed to become larger and larger.

In a sense, in this case, what is hidden inside this infinity is the whole complexity of a 3d space, at least of a flat one. What one finds is that hidden in this infinity, and carefully revealed by the scaling of the above amplitude with Emax, is all the information about the shape of the 3d object, i.e. of the possible 3d spacetime considered, and all the information about how this 3d spacetime has been constructed out of triangles. That’s lots of information!

Bonzom and Smerlak, in the work described at the seminar, have gone a very long way toward unraveling all this information, dwelling deeper and deeper into the hidden secrets of this particular infinity. Their work is developed in a series of papers, in which they offer a very elegant mathematical formulation of the problem and a new approach toward its solution, progressively sharpening their results and improving our understanding of these specific spin foam models for quantum gravity, of the way they depend on the shape and on the specific construction of each 3d spacetime, and of what shape and construction give, in some sense, the ‘bigger’infinity. Their work represented a very important contribution to an area of research that is growing fast and in which many other results, from other groups around the world, had already been obtained and are still being obtained nowadays.

There is even more. The analogy with particle processes in quantum field theory can be made sharper, and one can indeed study peculiar types of field theories, called ‘group field theories’, such that the above amplitude is indeed generated by the theory and assigned to the specific process, as in spin foam models, and at the same time all possible processes are taken into account, as in standard quantum field theories for particles.

This change of framework, embedding the spin foam model into a field theory language, does
not change much the problem of the divergence of the sum over the edge lengths, nor its infinite result.
And it does not change the information about the shape of space encoded in this infinity. However, it changes the perspective by which we look at this infinity and at its hidden secrets. In fact, in this new context, space and space-time are truly dynamical, all possible spaces and space-times have to be considered together and on equal footing and compete in their contribution to the total probability for a certain transition from one configuration of quantum space to another. We cannot just choose one given shape, do the calculation and be content with it (once we dealt with the infinity resulting from doing the calculation naively). The possible space-times we have to consider, moreover, include really weird ones, with billions of holes and strange connections from one regions to another, and 3d objects that do not really look like sensible space-times at all, and so on. We have to take them all into account, in this framework. This is of course an additional technical complication. However, it is also a fantastic opportunity. In fact, it offers us the chance to ask and possibly answer a very interesting question: why is our space-time, at least at our macroscopic scale, the way it is? Why does it look so regular, so simple in its shape, actually as simple as a sphere is? Try! we can consider an imaginary loop located anywhere in space and shrink it to a point making it disappear without any trouble, right? If the dynamics of quantum space is governed by a model (spin foam or group field theory) like the ones described, this is not obvious at all, but something to explain. Processes that look as nice as our macroscopic space-time are but a really tiny minority among the zillions of possible space-times that enter the sum we discussed, among all the possible processes that have to be considered in the above calculations. So, why should they ‘dominate’ and end up being the truly important ones, those that best approximate our macroscopic space-time? Why and how do they ‘emerge’ from the others and originate, from this quantum mess, the nice space-time we inhabit, in a classical, continuum approximation? What is the true quantum origin of space-time, in both its shape and geometry? The way the amplitudes grow with the increase of Emax is where the answer to these fascinating questions lies.

The answer, once more, is hidden in the very same infinity that Bonzom, Smerlak, and their many quantum gravity colleagues around the world are so bravely taming, studying, and, step by step, understanding.

Spinfoam cosmology with the cosmological constant

by David Sloan, Institute for Theoretical Physics, Utrecht University, Netherlands.

• Francesca Vidotto, CNRS Marseille

Title: Spinfoam cosmology with the cosmological constant
PDF of the slides (3 MB)
Audio [.wav 26MB], Audio [.aif 2MB].

Current observations of the universe show that it appears to be expanding. This is observed through the red-shift - a cosmological Doppler effect - of supernovae at large distances. These giant explosions provide a 'standard candle', a fixed signal whose color indicates relative motion to an observer. Distant objects, therefore appear not only to be moving away from us, but accelerating as they do so. This acceleration cannot be accounted for in a universe filled with 'ordinary' matter such as dust or radiation. To provide acceleration there must be a form of matter which has negative pressure. The exact nature of this matter is unknown, and hence it is referred to as being 'dark energy'.

 An image of the remnants of the Tycho type Ia supernova as

recorded by NASA's Spitzer observatory and originally observed by

Tycho Brahe.

According to the standard model of cosmology, 73% of the matter content of the universe consists of dark energy. It is the dominant component of the observable universe, with dark matter making up most
of the remainder (ordinary matter that makes up stars, planets, and nebulae comprises just 4%). In cosmology the universe is assumed to be broadly homogeneous and isotropic, and therefore the types of matter
present are usually parametrized by the ratio (w) of their pressure to energy. Dark energy is unlike normal matter as it exhibits negative pressure. Indeed in observations recently made by Reiss et al. this ratio has been determined to be -1.08 ± 0.1. There are several models which attempt to explain the nature of dark energy. Among them are Quintessence which consists of a scalar field whose pressure varies with time, and void (or Swiss-cheese) models which seek to explain the apparent expansion as an effect of large scale inhomogeneities.However, the currently favored model for dark energy is that of the cosmological constant, for which w=-1.

The cosmological constant has an interesting history as a concept in general relativity (GR). Originally introduced by Einstein, who noted there was the freedom to introduce it in the equations of the theory,  it was an attempt to counteract the expansion of the universe that appeared in general relativistic cosmology. It should be remembered that at that time it was thought the universe was static. The cosmological constant was quickly shown to be insufficient to lead to a stable, static universe. Worse, later observations showed the universe did expand as general relativistic cosmology seemed to suggest. However, the freedom to introduce this new parameter into the field equations of GR remained of theoretical interest, its cosmological solutions yielding (anti) DeSitter universes which can have a different topology to the flat cases. The long-term fate of the universe is generally determined by the cosmological constant - for large enough positive values the universe will expand indefinitely, accelerating as it does so. For negative values the universe will eventually recollapse, leading to a future 'big crunch' singularity. Recently through supernovae observations the value of the cosmological constant has been determined to be small yet positive. In natural (Planck) units, its value is 10^(-120), a number so incredibly tiny that it appears unlikely to have occurred by
chance. This 'smallness' or 'fine tuning' problem has elicited a number of tentative explanations ranging from anthropic arguments (since much higher values would make life impossible) to virtual wormholes, however as yet there is no well accepted answer.

The role of the cosmological constant can be understood in two separate ways - it can be considered either as a piece of the geometry or matter components of the field equations. As a geometrical entity it can be considered just as one more factor in the complicated way that geometry couples to matter, but as matter it can be associated with a 'vacuum' energy of the universe: energy associated with empty space. It is this dual nature that makes the cosmological constant an ideal test candidate for the introduction of matter into fundamental theories of gravity. The work of Bianchi, Krajevski, Rovelli and Vidotto, discussed in the ILQG seminar, concerns the addition of this term into the spin-foam cosmological models. Francesca describes how
one can introduce a term which yields this effect into the transition amplitudes (a method of calculating dynamics) of spin-foam models. This new ingredient allows Francesca to cook up a new model of cosmology within the spin-foam cosmology framework. When added to the usual recipe of a dipole graph, vertex expansions, and coherent states, the results described indeed appear to match well with the description
of our universe on large scales. The inclusion of this new factor brings insight from quantum deformed groups, which have been proposed as a way of making the theory finite.

This is an exciting development, as the spin-foam program is  'bottom-up' approach to the problem of quantum gravity. Rather than beginning with GR as we know it, and making perturbations around solutions, the spin-foam program starts with networks representing the fundamental gravitational fields and calculates dynamics through a foam of graphs interpolating between two networks. As such, recovering known physics is not a sure thing ahead of time. The results discussed in Francesca's seminar provide a firmer footing for understanding the cosmological implications of the spin-foam models and take these closer to observable physics.

Quantum deformations of 4d spin foam models

by Hanno Sahlmann, Asia Pacific Center for Theoretical Physics and Physics Department, Pohang University of Science and Technology, Korea.

• Winston Fairbairn, Hamburg University

Title: Quantum deformation of 4d spin foam models
PDF of the slides (300k)
Audio [.wav 36MB], Audio [.aif 3MB].

The work Winston Fairbairn talked about is very intriguing because it brings together a theory of quantum gravity, and some very interesting mathematical objects called quantum groups, in a way that may be related to the non-zero cosmological constant that is observed in nature! Let me try to explain what these things are, and how they fit together.

Quantum groups

A group is a set of things that you can multiply with each other to obtain yet another element of the group. So there is a product. Then there also needs to be a special element, the unit, that when multiplied with any element of the group, just gives back the same element. And finally there needs to be an inverse to every element, such that if one multiplies an element with its inverse, one gets the unit. For example, the integers are a group under addition, and the rotations in space are a group under composition of rotations. Groups are one of the most important mathematical ingredients in physical theories because they describe the symmetries of a physical system. A group can act in different ways on physical systems. Each such way is called a representation.

Groups have been studied in mathematics for hundreds of years, and so a great deal is known about them. Imagine the excitement when it was discovered that there exists a more general (and complicated) class of objects that nevertheless have many of the same properties as groups, in particular with respect to their mathematical representations. These objects are called quantum groups. Very roughly speaking, one can get a quantum group by thinking about the set of functions on a group. Functions can be added and multiplied in a natural way. And additionally, the group product, the inversion and the unit of the group itself, induce further structures on the set of functions in the group.

The product of functions is commutative - fg and gf are the same thing. But one can now consider set of functions that have all the required extra structure to make them set of functions acting over a group - except for the fact that the product is now not commutative anymore. Then the elements cannot be functions on a group anymore -- in fact they can't be functions at all. But one can still pretend that they are “functions” on some funny type of set: A quantum group. 

Particular examples of quantum groups can be found by deforming the structures one finds for ordinary groups. In these examples, there is a parameter q that measures how big the deformations are. q=1 corresponds to the structure without deformation. If q is a complex number with q^n=1 for some integer n (i.e., q is a root of unity), the quantum groups have particular properties. Another special class of deformations is obtained for q a real number. Both of these cases seem to be relevant in quantum gravity.

Quantum gravity

Finding a quantum theory of gravity is an important goal of modern physics, and it is what loop quantum gravity is all about. Since gravity is also a theory of space, time, and how they fit together in a space-time geometry, quantum gravity is believed to be a very unusual theory, one in which quantities like time and distance come in discrete bits, (atoms of space-time, if you like) and are not all simultaneously measureable.

One way to think about quantum theory in general is in terms of what is known as "path integrals". Such calculations answer the question of how probable it is that a given event (for example two electrons scattering off each other) will happen. To compute the path integral, one must sum up complex numbers (amplitudes), one for each way that the thing under study can happen. The probability is then given in terms of this sum. Most of the time this involves infinitely may possible ways, the electrons for example can scatter by exchanging one photon, or two, or three, or..., the first photon can be emitted in infinitely many different places, and have different energies etc. Therefore computing path integrals is very subtle, needs approximations, and can lead to infinite values. Path integrals were introduced into physics by Feynman. Not only did he suggest to think about quantum theory in terms of these integrals, he also introduced an ingenious device useful for their approximate calculation. To each term in an approximate calculation of some particular process in quantum field theory, he associated what we now call its Feynman diagram. The nice thing about Feynman diagrams is that they not only have a technical meaning. They can also be read as one particular way in which a process can happen. This makes working with them very intuitive.

(image from Wikipedia)

It turns out that  loop quantum gravity can also be formulated using some sort of path integrals. This is often called spin foam gravity. The spin foams in the name are actually very nice analogs to Feynman diagrams in ordinary quantum theory: They are also a technical device in an approximation of the full integral - but as for Feynman diagrams, one can read them as a space-time history of a process - only now the process is how space-time itself changes!

Associating the amplitude to a given diagram usually involves integrals. In the case of quantum field theory there is an integral over the momentum of each particle involved in the process. In the case of spin foams, there are also integrals or infinite sums, but those are over the labels of group representations! This is the magic of loop quantum gravity: Properties of quantized space-time are encoded in group representations. The groups most relevant for gravity are known as technically as SL(2,C) -- a group containing all the Lorentz transformations, and SU(2), a subgroup related to spatial rotations.  

Cosmological constant

In some theories of gravity, empty space “has weight”, and hence influences the dynamics of the universe. This influence is governed by a quantity called the cosmological constant. Until a bit more than ten years ago, the possibility of a non-zero cosmological constant was not considered very seriously, but to everybody’s surprise, astronomers then discovered strong evidence that there is a positive cosmological constant. Creating empty space creates energy! The effect of this is so large that it seems to dominate cosmological evolution at the present epoch (and there has been theoretical evidence for something like a cosmological constant in earlier epochs, too). Quantum field theory in fact predicts that there should be energy in empty space, but the observed cosmological constant is tremendously much smaller than what would be expected. So the explaining the observed value of the cosmological constant presents quite a mystery for physics.

Spin foam gravity with quantum groups

Now I can finally come to the talk. As I've said before, path integrals are complicated objects, and infinities do crop up quite frequently in their calculation. Often these infinities are a due to problems with the approximations one has made, and sometimes several can be canceled against each other, leaving a finite result. To analyze those cases, it is very useful to first consider modifications of the path integral that remove all infinities, for example by restricting the ranges of integrations and sums. This kind of modification is called "introducing a regulator", and it certainly changes the physical content of the path integral. But introducing a regulator can help to analyze the situation and rearrange the calculation in such a way that in the end the regulator can be removed, leaving a finite result. Or one may be able to show that the existence of the regulator is in fact irrelevant at least in certain regimes of the theory.

Now back to gravity: For the case of Euclidean (meaning a theory of pure space rather than a theory of space-time, this is unphysical but simplifies certain calculations) quantum gravity in three dimensions, there is a nice spinfoam formulation due to Ponzano and Regge, but as can be anticipated, it gives divergent answers in certain situations. Turaev and Viro then realized that replacing the group by its quantum group deformation at a root of unity furnishes a very nice regularization. First of all, it does what a regulator is supposed to do, namely render the amplitude finite. This happens because the quantum group in question, with q a root of unity, turns out to have only finitely many irreducible representations, so the infinite sums that were causing the problems are now replaced by finite sums. Moreover, as the original group was only deformed, and not completely broken, one expects that the regulated results stay reasonably close to the ones without regulator. In fact, something even nicer happens: It turned out (work by Mizoguchi and Tada) that the amplitudes in which the group is replaced by its deformation into a quantum group correspond to another physical theory -- quantum gravity with a (positive) cosmological constant! The deformation parameter q is directly related to the value of the constant. So this regulator is not just a technical tool to make the amplitudes finite. It has real physical meaning.

Winston's talk was not about three dimensional gravity, but on the four dimensional version - the real thing, if you like. He was considering what is called the EPRL vertex, a new way to associate amplitudes to spin foams, devised by Engle, Pereira, Rovelli and Livine, which has created a lot of excitement among people working on loop quantum gravity. The amplitudes obtained this way are finite in a surprising number of circumstances, but infinities are nevertheless encountered as well. Winston Fairbairn, together with Catherine Meusburger (and, independently, Muxin Han), were now able to write down the new vertex function in which the group is replaced by a deformation into a quantum group. In fact, they developed a nice graphical calculus to do so. What is more, they were able to show that it gives finite amplitudes. Thus the introduction of the quantum group does its job as a regulator.

As for the technical details, let me just say that they are fiercely complicated. To appreciate the intricacy of this work, you should know that the group SL(2,C) involved is what is known as non-compact, which makes its quantum group deformations very complicated and challenging structures (intuitively, compact sets have less chance of producing infinities than non-compact ones). Also, the EPRL vertex function relies on a subtle interplay between SU(2) and SL(2,C). One has to understand this interplay on a very abstract level to be able to translate it to quantum groups. The relevant type of deformation in this case has a real parameter q. In this case, there are still infinitely many irreducible representations – but it seems that it is the quantum version of the interplay between SU(2) and SL(2,C) that brings about the finiteness of the sums.

Thanks to this work, we now have a very interesting question on our hands: Is the quantum group deformation of the EPRL theory again related to gravity with a cosmological constant? Many people bet that this is the case, and the calculations to investigate this question have already begun, for example in a recent preprint by Ding and Han. Also, this begs the question of how fundamentally intertwined quantum gravity is with quantum groups. There were some interesting discussions about this already during and after the talk. At this point, the connection is still rather mysterious on a fundamental level.

Observational signatures of loop quantum cosmology?

by Edward Wilson-Ewing, Penn State

• Ivan Agullo, March 29th 2011. Observational signatures of loop quantum cosmology? PDF of the slides, and audio in either .wav (40MB) or .aif format (4MB).

In the very early universe the temperature was so high that electrons and protons would not combine to form hydrogen atoms but rather formed a plasma that made it impossible for photons to travel significant distances as they would continuously interact with the electrons and protons.  However, as the early universe expanded, it cooled and, 380 000 years after the Big Bang, the temperature became low enough for hydrogen atoms to form in a process called recombination.  At this point in time, it became possible for photons to travel freely, as the electrons and protons had combined to become electrically neutral atoms.  It is possible today to observe the photons from that era that are still travelling through the universe: these photons form what is called the cosmic microwave background (CMB).  By observing the CMB, we are in fact looking at a photograph of what the universe looked like only 380 000 years after the Big Bang!  Needless to say, the detection of the CMB was an extremely important discovery and the study of it has taught us a great deal about the early universe.

The existence of the CMB was first predicted in 1948 by George Gamow, Ralph Adler and Robert Herman, when they estimated its temperature to be approximately 5 degrees Kelvin.  Despite this prediction, the CMB was not detected until Arno Penzias and Robert Wilson made their Nobel Prize-winning discovery in 1964.  Ever since then, there have been many efforts to create better radio telescopes, both Earth- and satellite-based, that would provide more precise data and therefore more information about the early universe.  In the early 1990s the COBE (COsmic Background Explorer) satellite's measurements of the small anisotropies in the CMB were considered so important that two of COBE's principal investigators, George Smoot and John Mather, were awarded the 2006 Nobel Prize.  The state-of-the-art data today comes from the WMAP (Wilkinson Microwave Anisotropy Probe) satellite and there is already another satellite that has been taking data since 2009.  This satellite, called Planck, has a higher sensitivity and better angular resolution than WMAP ,and its improved map of the CMB is expected to have been completed by the end of 2012.

The CMB is an almost perfect black body and its temperature has been measured to be 2.7 degrees Kelvin.  As one can see in the figure below, the black body curve of the CMB is perfect: all of the data points lie right on the best fit curve.  It is possible to measure the CMB's temperature in every direction and it has been found that it is the same in every direction (what is called isotropic) up to one part in 100 000.

Even though the anisotropies are very small, they have been measured quite precisely by the WMAP satellite, and one can study how the variations in temperature are correlated by their angular separation in the sky.  This gives the power spectrum of the CMB, where once again theory and experiment agree quite nicely:

In order to obtain a theoretical prediction about what the power spectrum should look like, it is important to understand how the universe behaved before recombination occurred.  This is where inflation, an important part of the standard cosmological model, comes in.  The inflationary epoch occurs very soon after the universe leaves the Planck regime (where quantum gravity effects may be important), and during this period the universe's volume increases by a factor of approximately e^(210) in the very short time of about 10^(-33) seconds (for more information about inflation, see the previous blog post).  Inflation was first suggested as a mechanism that could explain why (among other things) the CMB is so isotropic: one effect of the universe's rapid expansion during inflation is that the entire visible universe today occupied a small volume before the beginning of inflation and had had time to enter into causal contact and thermalize.  This pre-inflation thermalization can explain why, when we look at the universe today, the temperature of the cosmic microwave background is the same in all directions.  But this is not all: using inflation, it is also possible to predict the form of the power spectrum.  This was done well before it was measured sufficiently precisely by WMAP and, as one can see in the graph above, the observations match the prediction very well!  Thus, even though inflation was introduced to explain why the CMB's temperature is so isotropic, it also explains the observed power spectrum.  It is especially this second success that has ensured that inflation is part of the standard cosmological model today.

However, there remain some issues that have not been resolved in inflation.  For example, at the beginning of inflation, it is assumed that the quantum fields are in a particular state called the Bunch-Davies vacuum.  It is then possible to evolve this initial state in order to determine the state of the quantum fields at the end of inflation and hence determine what the power spectrum should look like.  Even though the predicted power spectrum agrees extremely well with the observed one, it is not entirely clear why the quantum fields should be in the Bunch-Davies vacuum at the onset of inflation.  In order to explain this, we must try to understand what happened before inflation started and this requires a theory of quantum gravity.

Loop quantum cosmology is one particular quantum gravity theory which is applied to the study of our universe.  There have been many interesting results in the field over the last few years: (i) it has been shown in many models that the initial big bang singularity is replaced by a “bounce” where the universe contracts to a minimal volume and then begins to expand again; (ii) it has also been shown that quantum gravity effects only become important when the space-time curvature reaches the Planck regime, therefore classical general relativity is an excellent approximation when the curvature is less than the Planck scale; (iii) the dynamics of the universe around the bounce point are such that inflation occurs naturally once the space-time curvature leaves the Planck regime.

The goal of the project presented in the ILQGS talk is to use loop quantum cosmology in order to determine whether or not the quantum fields should be in the Bunch-Davies vacuum at the onset of inflation.  More specifically, the idea is to choose carefully the initial conditions at the bounce point of the universe (rather than at the beginning of inflation) and then study how the state of the fields evolves as the universe expands in order to determine their state at the beginning of inflation.  Now one can ask: Does this change the state of the quantum fields at the onset of inflation?  And if so, are there any observational consequences?  These are the questions addressed in this presentation.

Inflation and observational constraints on loop quantum cosmology

by Ivan Agulló, Penn State

• Gianluca Calcagni, Inflationary observables and observational constraints on loop quantum cosmology January 18th 2011. PDF of the slides, and audio in either .wav (40MB) or .aif format (4MB).

Cosmology has achieved a remarkable progress in the recent years. The proliferation of meticulous observations of the Universe in the last two decades has produced a significant advance in our understanding of its large scale structure and of its different stages of evolution. The precision attained in the observations already made, and in the observations expected in the near future, is such that the Cosmos itself constitutes a promising "laboratory" to obtain information about fundamental physics. The obvious drawback is that, unlike what happens in common  laboratories on earth, such as the famous Large Hadron Collider at CERN, our Universe has to be observed as it is, and we are not allowed to select and modify the parameters of the "experiment". The seminar given by Gianluca Calcagni, based on results obtained in collaboration with M. Bojowald and S. Tsujikawa, shows an analysis of the effects that certain aspects of quantum gravity, in the context of Loop Quantum Cosmology, could produce on observations of the present Universe.

One of the important pieces of the current understanding of the Universe is the mechanism of inflation. The concept of inflation generically makes reference to the enormous increase of some quantity in a short period of time. It is a concept that is surely familiar to everyone, because we all have experienced an epoch when, for instance, house prices have experienced an alarming growth in a brief period. In the case of cosmological inflation the quantity increasing with time is the size of the Universe. Inflation considers that there was a period in the early Universe in which its volume increased by a factor of arround 10⁷⁸ (a 1 followed by 78 zeros!) in a period of time of about 10^-36 seconds. There is no doubt that, fortunately, this inflationary process is more violent than anything that we experience in our everyday life. The inflationary mechanism  in cosmology was introduced by Alan Guth in 1981, and was formulated in its modern version by A. Linde, A. Abrecht, P. Steinhard a year later. Guth realized that a huge expansion would make the Universe look almost flat and highly homogeneous for its inhabitants, without requiring it had been like that since its origin. This is consistent with observations of our Universe, which looks like highly homogeneous on large scales; and we know, by observing the cosmic microwave background (CMB), was even more homogeneous in the past. The CMB constitutes a "photograph" of the Universe when it was 380000 years old (a teenager compared with its current age of about 14000000000 years) and shows that the inhomogeneities existing at that time consisted of tiny variations (of 1 part in 100000) of its temperature. These small fluctuations are the origin of the inhomogeneities that we observe today in form of galaxies cluster, galaxies, stars, etc.

However, a few years after the proposal of inflation, several researchers (Mukhanov, Hawking, Guth, Pi, Starobinsky, Bardeen, Steinhardt and Turner) realized that inflation may provide something more valuable than a way of understanding the homogeneity and flatness of the observable Universe. Inflation provides a natural mechanism for generating the small inhomogeneities we observe in the CMB through one of the most attractive ideas in contemporary physics. A violent expansion of the Universe is able to amplify quantum vacuum fluctuations (that exist as a consequece of the Heisenberg’s uncertainty principle), and spontaneously produce tiny density fluctuations. In that way, General Relativity, via the exponential expansion of the Universe, and Quantum Mechanics, via the uncertainty principle, appear together (but not scrambled) in the game to generate a spectrum of primordial cosmic inhomogeneities out from the vacuum. This spectrum constitutes the "seed" that, by the effect of gravity, will later evolve into the temperature fluctuations of the CMB and then into the structures that we observe today in our Universe, from galaxy clusters to ourselves. The statistical properties of the temperature distribution of the CMB, analyzed in great detail by the WMAP satellite in the last decade, confirm that this picture of the genesis of our Universe is compatible with observations. Although there is not enough data to confirm the existence of an inflationary phase in the early stages of the Universe, inflation is one of the best candidates in the landscape of contemporary physics to explain the origin of the cosmic structures.

The mechanism of inflation opens a window of interesting possibilities for both theoretical and experimental physicists. The increase of the size of the Universe during inflation is such that the radius of an atom would expand to reach a distance that light would take a year to travel. This means that, if there was a period of inflation in the past, by observing the details of small temperature fluctuations in the CMB, we are actually getting information about physical processes that took place at extremely small distances or, equivalently, at very large energies. In particular, inflation predicts that the origin of the CMB temperature variations are generated from quantum vacuum fluctuations when the energy density of the Universe was about 10^-11 times the Planck density (the Planck density corresponds to 5·10¹¹³ Jules per cubic meter). The energy density that the Large Hadron Collider at CERN is going to reach is around 10^-60 times the Planck density, that is 49 orders of magnitude smaller! In this sense, the observation of our own Universe is a promising way to reveal information about physical theories that only become apparent at very high energies, as it is the case of quantum gravity. This fact has motivated experts in quantum gravity to focus their research on the predictions of potential observable signatures of their theories in cosmology, as shown in this seminar by Gianluca Calcagni.

Gianluca Calcagni shows in this seminar an analysis of the effects that certain aspects of quantum gravity, from the perspective Loop Quantum Cosmology (LQC), could produce on the generation of primordial fluctuations during inflation. Generally, LQC introduces two types of corrections to the equations describing the evolution of cosmic inhomogeneities; the so-called holonomy corrections and inverse volume corrections. This seminar focuses on the latter type, leaving the former for future work. Gianluca shows that it is possible to obtain the equations describing cosmic inhomogeneities during the inflationary epoch including inverse volume effects in LQC consistently (in the case that these corrections are small). With these equations it is possible then to recalculate the properties of the temperature distribution of the CMB including such LQC corrections. Generically, the effects that quantum aspects of gravity introduce into the classical equations are relevant when the scale of energy density is close to the Planck scale, and quickly disappear at lower scales. One would expect, therefore, that at the energy density at which inflation occurs, which is eleven orders of magnitude below the Planck scale, the effects of quantum gravity would be suppressed by a factor of 10^-11. The authors of this work argue that, surprisingly, this is not the case, and inverse volume corrections may be larger. In summary, the conclusions of this seminar suggests that even though the effects that quantum aspects of gravity have on the CMB are small, cosmological observations can put upper bounds on the magnitude of the corrections coming from quantum gravity that may be closer to theoretical expectation than what one would expect.

Although there is still a lot of work to do, the observation of our Universe via the cosmic microwave background and the distribution of galaxies is shown as a promising way to obtain information about physical processes where the relationship of Quantum Mechanics and General Relativity plays a major role. In this sense, it may be the Universe itself which give us a helping hand toward the understanding of the fundamental laws of physics.